
真空崩壊の応用は非常に幅広く、とても1つのガイドで全てをご紹介することはできません。そこで本ページでは私の独断と偏見で選出したいくつかのシナリオについて解説します。興味をそそられるものがあれば、ぜひ参考文献をご覧ください。
素粒子物理学には「金字塔」と評される理論が存在します。これは素粒子標準模型と呼ばれており、その理論計算は観測実験の結果と非常に高い精度で一致することが確かめられています。2012年には大型ハドロン加速機(Large Hadron Collider)によるヒッグス粒子の直接観測も達成され、その妥当性はより一層堅固なものになりました。
一方で、「標準模型の真空は安定ではないのではないか?」とも囁かれてきました[1]。より専門的には「我々が存在する現在の電弱真空は準安定なのではないか?」という主張です。実は、近年のトップクォーク質量の測定により、この主張は真であることがわかってきました。つまり、我々の宇宙は偽真空であり、有限の時間で崩壊する可能性を孕んでいるのです[注]。
この電弱真空の崩壊はよく宇宙の終末のシナリオとして各種メディアでも取り上げられています。「数学的定式化」でも解説した通り、真空崩壊が起こると、真真空の泡が光速に近いスピードで迫ってきます。この泡に触れるとどうなってしまうのでしょうか。名古屋大学の庄司先生は次のように説明します[2]。
「一度壁に触れたら最後,一瞬でバラバラに分解され,壁の一部になってしまうであろう.この泡が宇宙 を覆い,宇宙の構造を破壊し尽くした時,我々の宇宙は終焉を迎える.」
我々はこの恐ろしいシナリオの前に、ただ悲観するしかないのでしょうか。実は、そこまで心配する必要はない、というのが現代物理学の結論です。具体的な我々の宇宙の寿命は「数学的定式化」でご紹介した経路積分の方法によって見積もることができ、最新の計算によると、標準模型の真空の寿命は我々の宇宙年齢よりも数百桁長いことが分かっています[3]。下図を見ると分かる通り、準安定とは言えど、本当にギリギリのところで準安定な真空となっているようです。

図6 トップクォークとヒッグス粒子の質量に対する崩壊率を描いたもの。色分けは真空の安定性に対応しており、青色が完全に不安定、赤色が準安定、黄色が完全に安定な真空であることを表している。観測結果によると、標準模型の真空(電弱真空)は緑色の楕円の領域に位置し、ギリギリ準安定であるようです。[3]より抜粋。
[注] この主張は標準模型の枠組み内に限った議論であることに注意する必要があります。我々の生きている真空が絶対的に安定であるか、それとも不安定であるかを決定するには、究極的には万物の理論をもって、他のあらゆる真空のエネルギーが我々の真空のそれと比較して大きいか否かを比較する必要があります。
[1] M. Sher, "Electroweak Higgs Potentials and Vacuum Stability," Phys.Rept. 179 (1989) 273-418.
https://doi.org/10.1016/0370-1573(89)90061-6
[2] 庄司 裕太郎, 「真空の寿命」, 日本物理学会誌, 74, 3, 128-136 (2019).
https://doi.org/10.11316/butsuri.74.3_128
[3] P. Baratella, M. Nemevšek, Y, Shoji, K. Trailović, L. Ubaldi, "Revising the full one-loop gauge prefactor in electroweak vacuum stability," Phys.Rev.Lett. 134 (2025) 1, 011601.
https://doi.org/10.1103/PhysRevLett.134.011601
「数学的定式化」で見たように、真空崩壊の起こる確率は指数関数(\(e^{-B/\hbar}\))で抑えられているので、そうそう起こるものではありません。標準模型の真空の寿命が非常に長いのも、このためです。しかし、もっと現実的な宇宙を考えるとどうなるのでしょうか?
我々の生きる宇宙は非常に複雑です。地球や火星のような惑星、自ら光り輝く恒星、星雲などなど、様々な登場人物がいます。これらの存在も加味すれば、より正確に真空の寿命を計算できるように思えます。2014年、イギリスの研究チームがある興味深い研究を発表しました。それは、宇宙に存在するブラックホールが真空崩壊を促進するかもしれない、というものです[1]。彼らは、ブラックホールが存在するような膨張宇宙(シュワルツシルト・ドジッター時空)を考え、その崩壊率を計算しました。その結果、粒子程度の大きさの小さなブラックホールが存在すると、その周囲での崩壊確率が著しく増幅されることを発見したのです。
彼らのアイデアは大気中での雲の形成や、砂粒入りの炭酸水中での発泡に似ています。炭酸水中では絶えず二酸化炭素の泡が出現していますが、砂粒を混入した際の様子を注意深く観察すると、その砂粒の周りで特に泡の形成数が多いことがわかります。ブラックホールが存在する場合も同様で、ブラックホールの持つエントロピーの一部が解放されることにより、崩壊がより促進されます(図7)。

図7 ブラックホールを中心に崩壊が促進される。[2]より抜粋。
実は、ブラックホールに限らず、多くの物体でこのような「触媒効果」が確認されており、特に初期宇宙論の文脈で精力的に研究が進められています。その詳細については、「不安定性の増強」にてご紹介することにしましょう。
[1] R. Gregory, I. G. Moss, B. Withers, "Black holes as bubble nucleation sites," JHEP 03 (2014) 081 [arXiv: 1401.0017 [hep-th]].
https://doi.org/10.1007/JHEP03(2014)081
[2] I. G. Moss, R. Gregory, "Higgs Cosmology and Dark Matter," PoS EDSU2018 (2018) 010 [arXiv: 1809.00131 [hep-ph]].
https://doi.org/10.22323/1.335.0010
宇宙はどこから始まったのか
これは現代宇宙論における最も重要な問題の1つです。長年の宇宙観測により、我々の住む宇宙は加速膨張していることがわかっています。これは時間を遡っていくと、いずれ空間の大きさがゼロになってしまうような、いわゆる特異点に突き当たってしまうことを示唆しています(例えば[1]を参照)。我々の宇宙は一体どのようにして誕生したのでしょうか。
現代宇宙論では、時空の自由度の存在しない「無」の状態から、量子効果によって時空が創世したと考えられています。この枠組みにおいて、宇宙創世を記述する2つの有力な仮説が存在します。1つは無境界仮説と呼ばれており、1983年にハートルとホーキングによって提唱されました[2]。この仮説は宇宙の時間発展を波動関数が虚時間の経路積分によって得られるとするもので、「(実時間を持つ時空中に)境界が無いのが境界条件」と言われることもあります。
もう1つがビレンキンのトンネリング仮説で、本ガイドの主題でもあるトンネル効果によって宇宙が創世したというものです[3]。ビレンキンのアイデアは"宇宙の波動方程式"を観察することにより理解できます。急に厨二病のようなワードが登場しましたね。"宇宙の波動方程式"、正式名称ホイーラー・ドウィット方程式は以下のような方程式です。
\(\left[-\hbar^{2}\frac{d^{2}}{da^{2}} + \left(\frac{3\pi}{2G} \right) \left(a^{2} - \ell^{-2}a^{4} \right) \right]\psi(a) = 0\)
方程式中の\(a\)はスケール因子と呼ばれる変数であり、素朴には宇宙のサイズを規定するものです。ホイーラー・ドウィット方程式は一般相対性理論を通常の量子力学と同じ手続きで量子化することで求めることができます。つまり、この方程式は量子力学において登場するシュレディンガー方程式の対応物とみなすことができます。ホイーラー・ドウィット方程式を解けば、宇宙の状態を記述する波動関数\(\psi(a)\)を求めることができ、この波動関数は「宇宙の波動関数」と呼ばれています。
さて、この方程式をグッと睨むと、\(\left(\frac{3\pi}{2G} \right) \left(a^{2} - \ell^{-2}a^{4} \right)\)の部分がポテンシャルのように見えてきます。1項目は宇宙の曲率、2項目は宇宙項からの寄与に相当するものです。この"ポテンシャル"をスケール因子\(a\)についてプロットすると下図のようになります。
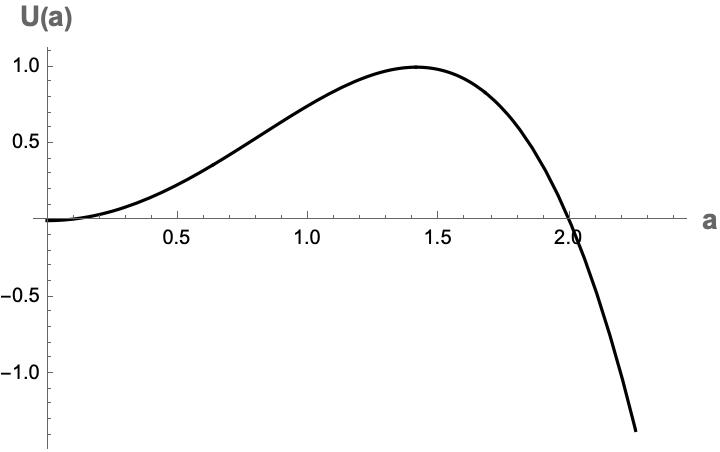
図8 ホイーラー・ドウィット方程式に現れる「ポテンシャル項」の概形
見覚えのある関数形をしていますね。これはまさにトンネリングを起こすようなポテンシャルの形をしています。ここで\(a=0\)というのはスケール因子、つまり宇宙のサイズがゼロの「無」に相当する部分です。ビレンキンの仮説におけるトンネリングとは、このポテンシャル障壁を透過することを指しています。
いずれの仮説が正しいのかについては、長年議論の的になってきたのですが、実は最近(2025年2月10日執筆時点)、日本のグループの研究によりトンネリング仮説の方が有力である可能性が示唆されました[4]。トンネル効果の物理は、我々の宇宙の始まりさえも解き明かしてしまうのかもしれません。
[1] 佐藤勝彦, 二間瀬敏史, 『宇宙論Ⅰ 宇宙の始まり』「シリーズ現代の天文学」, 日本評論社 (2008) (九大蔵書: https://hdl.handle.net/2324/1001238420).
[2] J. Hartle and S. W. Hawking, "Wave function of the universe," Phys.Rev.D 28 (1983) 2960.
https://doi.org/10.1103/PhysRevD.28.2960
[3] A. Vilenkin, "Creation of Universes from Nothing," Phys.Lett.B 117 (1982) 25-28.
https://doi.org/10.1016/0370-2693(82)90866-8
[4] M. Honda, H. Matsui, K. Okabayashi, T. Terada, "Resurgence in Lorentzian quantum cosmology: No-boundary saddles and resummation of quantum gravity corrections around tunneling saddle points," Phys.Rev.D 110 (2024) 8, 083508.
https://doi.org/10.1103/PhysRevD.110.083508
超弦理論はしばしば「万物の理論」の有力な候補として紹介されます。「万物の理論」というセンセーショナルな響きも相まって、よくメディアや科学館でも取り上げられることの多い理論です。「万物の理論」という呼称は少し誇張が過ぎるようにも感じますが、4つの基本相互作用を自然に内包するという点において統一理論として好ましい性質も備えています。また、その数理構造の奥深さも相まって現代の素粒子理論では一大研究テーマとなっています。
しかし、超弦理論も完璧ではありません。もし超弦理論が統一理論であるならば、標準模型や標準宇宙モデルのように実験事実を精度良く説明する理論をその枠組み内で導出できなければなりませんが、現状その試みが成功した例は皆無です。とりわけ、我々の住む宇宙と同じく加速膨張を引き起こすような真空(ドジッター真空)については、安定な真空としては構築できないのではないかという予想すら立てられている状況です[注]。
このように困難な状況において、2019年にとある興味深いシナリオが提案されました[1][2]。今日バブルコスモロジーと呼ばれているそのシナリオでは、宇宙定数が負の真空(アンチドジッター真空)から別のアンチドジッター真空への真空崩壊を考えます。

図9 アンチドジッター真空からアンチドジッター真空
このシナリオでは、我々の住む4次元よりも1次元高い5次元時空における真空崩壊を考えます。そうすると、真空崩壊の際に生じる泡の表面は4次元となり、そこに宇宙定数が正の宇宙が実現されます。高次元をイメージするのは簡単ではありませんが、私たちの世界(3次元空間)でシャボン玉(2次元球面)ができる過程を考えると理解しやすいかもしれません。先述した通りドジッター真空を超弦理論の枠組みで構築するのは非常に難しいものの、アンチドジッター真空については比較的容易に構築することができます。ゆえに、このシナリオは超弦理論的宇宙論(ストリング・コスモロジー)の分野に新たな道筋を提示するものとして、注目を集めています。
[注] ドジッター予想と呼ばれています。
[1] S. Banerjee, U. Danielsson, G. Dibietto, S. Giri, M. Schillo, "Emergent de Sitter Cosmology from Decaying Anti–de Sitter Space," Phys.Rev.Lett. 121 (2018) 26, 261301.
https://doi.org/10.1103/PhysRevLett.121.261301
[2] S. Banerjee, U. Danielsson, G. Dibietto, S. Giri, M. Schillo, "De Sitter cosmology on an expanding bubble," JHEP 10 (2019) 164.
https://doi.org/10.1007/JHEP10(2019)164
この世は10次元時空なのかもしれない、そんな絵空事のようなことが理論物理学では真剣に議論されています。
10次元というのは超弦理論の量子論的な無矛盾性から要請される数字です[注1]。量子重力理論を考えると、このような高次元時空が自然に姿を現します。しかし、実際の我々の観測している宇宙は4次元ですので、余計な6次元空間をどうにか処理しなければなりません。その際、理論物理学では「余剰次元空間は目に見えないぐらい小さなスケールまで丸め込まれているんだ」と考えます。これはコンパクト化と呼ばれる操作であり、超弦理論のような高次元理論から4次元有効理論を構築するのに欠かせない要素です。
仮にあらゆる課題をクリアして非常に優れた4次元の理論を作れたとしましょう。果たしてその理論は安心安全完璧な理論なのでしょうか。実はそうとも言い切れない事情が存在します。実は、コンパクト化された時空には、それ特有の不安定性が内在しているのです。
最も簡単な高次元真空として、5次元カルツァ・クライン真空を考えてみましょう。これは何の変哲もない平坦な4次元時空[注2]に、1つの余剰次元が付与されたような5次元時空です(図10)。この5番目の時空は先述したコンパクト化という操作によって円の形に丸め込まれています。この時空はちょっと「振動」を加えたぐらいではその構造を変えることはありません。少しカッコつけた言い方をすると、「摂動的に安定な真空」になっています。しかし、ずっと安定的に存在できるわけではありません。理論物理学のスーパースター、エドワード・ウィッテン[注3]によって、摂動的には安定であるカルツァ・クライン真空も非摂動的にはそうではないことが明らかになりました[1]。つまり、カルツァ・クライン真空も真空崩壊の危険性を抱えているのです。

図10 カルツァ・クライン真空の概念図。通常の4次元時空を1つの横軸に押し込めて描いている。5番目の時空はコンパクト化されており、有限のサイズ(コンパクトなサイズ)になっている。
ウィッテンの指摘した崩壊現象は、比喩的に「無の泡」(bubble of nothing)と呼ばれています。「無の泡」のダイナミクスは非直感的です。この崩壊が起こるとカルツァ・クライン真空中に時空の自由度が存在しないような、文字通りの「無の泡」が出現します(下図参照)。無の泡は光速に近い速さで膨張し、いずれカルツァ・クライン真空全体を覆い尽くしてしまいます。つまり、崩壊が起こったあとに残るのは、まさに「無」の空間です。

図11 Kaluza-Klein真空中に出現した「無の泡」。\(r\)は極座標表示をした場合の動径方向。
「無の泡」を念頭に置くと、超弦理論からトップダウンに構築した4次元時空も危ういのでは?と考えられます。実際、近年では弦理論的なセットアップでの「無の泡」の解析も進められています。しかし、今のところ何とも言えないのが現状です。実は「無の泡」による崩壊を引き起こすインスタントン解は、コンパクト化された時空であればいつでも構成できるというわけではありません。時空に超対称性があるか、物質粒子(フェルミオン)がいるか、エネルギー条件は成立しているかなどなど、あらゆる条件をクリアして初めて「無の泡」インスタントンは構成することができます。また、現実的なドジッター真空を構築するには特異点やゲージ場、ブレーンなどの多様な構成要素を絶妙にコントロールする必要があることもわかっています[注4]。これらを踏まえると、現実的な模型において「無の泡」による崩壊が起こるかどうかを知るには、まだまだ人類のテクノロジーが追いついていないと言わざるを得ません。
[注1] より専門的にはワイルアノマリーやローレンツアノマリーの相殺条件から臨界次元の10という数字が導出されます。
[注2] ミンコフスキー時空と呼ばれています。
[注3] E. Wittenについては、Cute.Guides「素粒子理論に至る道」のColumn7を参照。
[注4] マルダセナ・ニュネツの禁止定理
[1] E. Witten, "Instability of Kaluza-Klein Vacuum," Nucl.Phys.B 195 (1982) 481-492.
https://doi.org/10.1016/0550-3213(82)90007-4