★手計算とRで学ぶ統計学: 線形モデリング (回帰分析)

0. Home

1. データ分析初歩の初歩

1.1 実例でわかる！統計学の重要性

1.2 どのようにデータを取れば良いか

1.3 統計量の基本

1.4 頻出用語の定義確認

2. 統計的仮説検定の仕組み

3. 実験前のサンプルサイズ設計

4. \(t\)検定

4.1 1標本\(t\)検定

4.2 2標本\(t\)検定 (対応なし)

4.3 2標本\(t\)検定 (対応あり)

5. 相関分析

6. 分散分析

6.1一元配置分散分析 (対応なし)

6.2 一元配置分散分析 (対応あり)

7. 線形モデリング (回帰分析)

7.1 単回帰分析 (単回帰モデル)

7.2 重回帰分析 (重回帰モデル)

8. ノンパラメトリック検定

7.1 適合度の検定

7.2 独立性の検定

7.3 マン・ホイットニーのU検定

9. 実践！データ分析

9.1 Rを使った分析その前に

9.2 \(t\)検定

9.3 分散分析

9.4 線形モデリング (回帰分析)

9.5 ノンパラメトリック検定

10.「有意である」ってどういうこと？

11. おわりに

12. 参考文献

13. 付録

線形モデリング (回帰分析) は，過去のデータをもとに作成したモデルを用いて，未知の被説明変数を既知の説明変数 (単数または複数) から予測することを目的として行われます。
線形モデリング (回帰分析) の概念は以下の図のように表されます。

 

線形モデリングは，以下の図に示すように正規分布でない分布 (ポアソン分布など) に従うデータを扱うことのできる一般化線形モデル (Generalized Linear Model)，個体差などのランダム効果をモデルに組み込める一般化線形混合モデル (Generalized Linear Mixed Model) など様々な発展形がありますが，今回は最も単純な単回帰モデルを例に検定の流れを見ていきます。

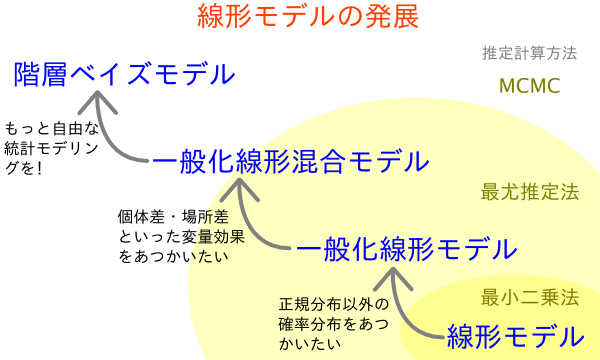
上の階層に進むにつれて，扱える確率分布や検討できる効果が増えていく。
(https://kuboweb.github.io/-kubo/ce/LinksGlm.html より引用)